INTRODUCTION AUX RESEAUX DE NEURONES FORMELS
Les réseaux de neurones formels (RNF), ou plus simplement réseaux de neurones (RN), constituent aujourd'hui une technique de traitement de données bien comprise et mâtrisée qui permet à l'ingénieur d'extraire, dans de nombreuses situations, le maximum d'informations pertinentes des données qu'il possède : commande de procédés, prédiction de propriétés, modélisation de fonctions, reconnaissance de formes, etc.
1. Définition des RN
De façon formelle, un RN est une fonction mathématique à laquelle sont associés des variables, un résultat, et des paramètres ajustables (poids). A partir d'un ensemble de données (mesures, résultats de calcul, indices économiques ou financiers, etc.), on peut ajuster un RN en choisissant convenablement ses paramètres.
Lorsque l'ajustement des paramètres a été effectué (apprentissage), le RN peut interpoler entre les données ; il peut ainsi prévoir le résultat de mesures qui n'ont pas encore été faites, expliquer des résultats obtenus dans le passé, etc.
Une fois convenablement ajusté, un RN constitue de fait un modèle statistique non linéaire des données.
2. Propriétés des RN
Les RN possèdent une propriété fondamentale qui les distingue des techniques classiques de traitement des données : ce sont des approximateurs universels parcimonieux. Cela signifie que pour obtenir un modèle non linéaire de précision de donnée, un RN a besoin de moins de paramètres ajustables que les méthodes de régression classiques (par exemple la régression polynomiale). Or le nombre de données nécessaires pour ajuster le modèle est directement lié au nombre de ses paramètres.
Par conséquent, un RN nécessite moins de données qu'une méthode de régression classique pour élaborer un modèle non linéaire de précision équivalente ; ou encore, un RN permet d'élaborer, à partir d'une même base de données, un modèle non linéaire plus précis. Ainsi de manière générale, dans le contexte de la modélisation non linéaire, un RN permet de tirer un meilleur parti des données dont on dispose.
Les RN présentent de plus trois caractéristiques particulièrement intéressantes. Ils sont :
-
adaptatifs : les RN sont entraînés à partir de données incorporées au système. Ainsi ils s'améliorent avec l'expérience ; leur réponse sera d'autant meilleure qu'ils emmagasinent des informations.
-
massivement parallèles : ceci suggère que les RN sauront prendre une décision en un temps très court.
-
capables de généralisation : un RN est capable de généralisation à partir des exemples de l'ensemble d'apprentissage.
3. Domaines d'application
Les grands domaines d'application des RN découlent naturellement des propriétés énoncées précédemment :
-
la régression non linéaire, ou modélisation de données statiques. Une immense variété de phénomènes statiques peuvent être caractérisés par une relation déterministe entre des causes et des effets ; les réseaux de neurones sont de bons candidats pour modéliser de telles relations à partir d'observations expérimentales, sous réserve que celles-ci soient suffisamment nombreuses et représentatives.
-
la modélisation de processus dynamiques non linéaires. Modéliser un processus consiste à déterminer un ensemble d'équations mathématiques qui décrivent le comportement dynamique du processus, i.e. l'évolution de ses sorties en fonction de l'évolution de ses entrées. Ce problème peut être avantageusement résolu par un RN, si le phénomène que l'on désire modéliser est non linéaire.
-
la commande de processus. Commander un processus signifie imposer un comportement défini à l'avance en fonction de signaux de commande ; l'ensemble commande / processus peut donc être considéré comme un système qui réalise une fonction (non linéaire) qu'un RN peut approcher.
-
la classification. En raison de leur propriété d'approximateurs universels, les RN sont capables d'estimer de manière précise la probabilité d'appartenance d'un objet inconnu à une classe parmi plusieurs possibles.
Conclusion
Les RN sont des outils puissants de traitement non linéaire des données qui n'ont pas encore atteint leur plein développement pour des raisons plus psychologiques que techniques, liées notamment aux connotations biologiques du terme et à leur relative nouveauté dans le monde industriel.
Nous avons exposé les propriétés fondamentales des RN qui justifient l'intérêt croissant qui leur est accordé : parcimonieux, adaptatifs, massivement parallèles, capables de généralisation. L'industrie doit pouvoir bénéficier de cette nouvelle avancée technologique.
Quelques ouvrages de référence
Neural Networks - a comprehensive
foundation, S. Haykin, Ed. Prentice Hall,
1999.
Neural networks for pattern recognition, C.
M. Bishop, Ed. Oxford University Press,
1995.
Réseaux de neurones et traitement du
signal, J. Hérault et C. Jutten, Ed. Hermès,
1994.
INTRODUCTION AUX MACHINES A VECTEURS DE SUPPORT (SVM)
A l'origine conçues pour les tâches de classification ou reconnaissance de formes, les SVM permettent également de traiter les problèmes de régression non linéaire. Nous privilégions ici leur intérêt pour la reconnaissance de formes (i.e. la découverte de caractéristiques communes dans un ensemble de données sans connaissance a priori du domaine). Dans ce contexte, l'acronyme SVM peut être judicieusement traduit par Séparateurs à Vaste Marge.
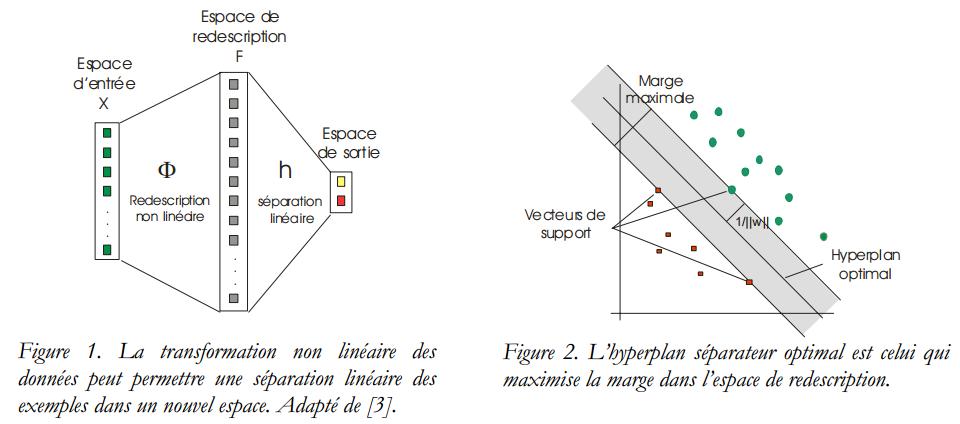
Voir lien : INTRODUCTION AUX MACHINES A VECTEURS DE SUPPORT (SVM)
